Physically consistent numerical solver for time-dependent Fokker-Planck equations

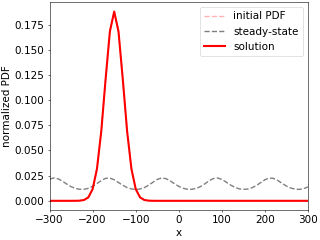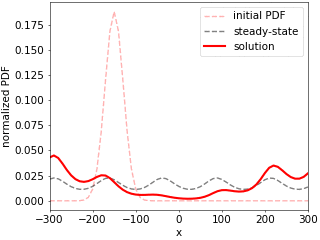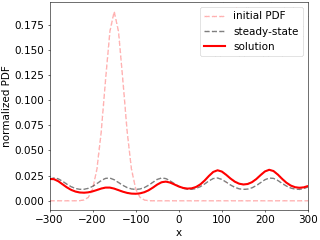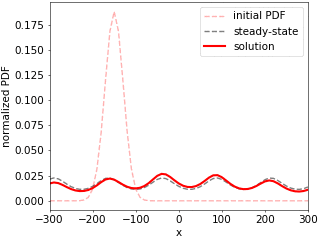
We present a simple thermodynamically consistent method for solving time-dependent Fokker--Planck equations (FPE) for over-damped stochastic processes, also known as Smoluchowski equations. It yields both transition and steady-state behavior and allows for computations of moment-generating and large-deviation functions of observables defined along stochastic trajectories, such as the fluctuating particle current, heat and work. The key strategy is to approximate the FPE by a Master equation with transition rates in configuration space that obey a local detailed balance condition for arbitrary discretization. Its time-dependent solution is obtained by a direct computation of the time-ordered exponential, representing the propagator of the FPE, by summing over all possible paths in the discretized space. The method thus not only preserves positivity and normalization of the solutions, but also yields a physically reasonable total entropy production, regardless of the discretization. To demonstrate the validity of the method and to exemplify its potential for applications, we compare it against Brownian-dynamics simulations of a heat engine based on an active Brownian particle trapped in a time-dependent quartic potential.

PDF Abstract