Deterministic particle flows for constraining stochastic nonlinear systems
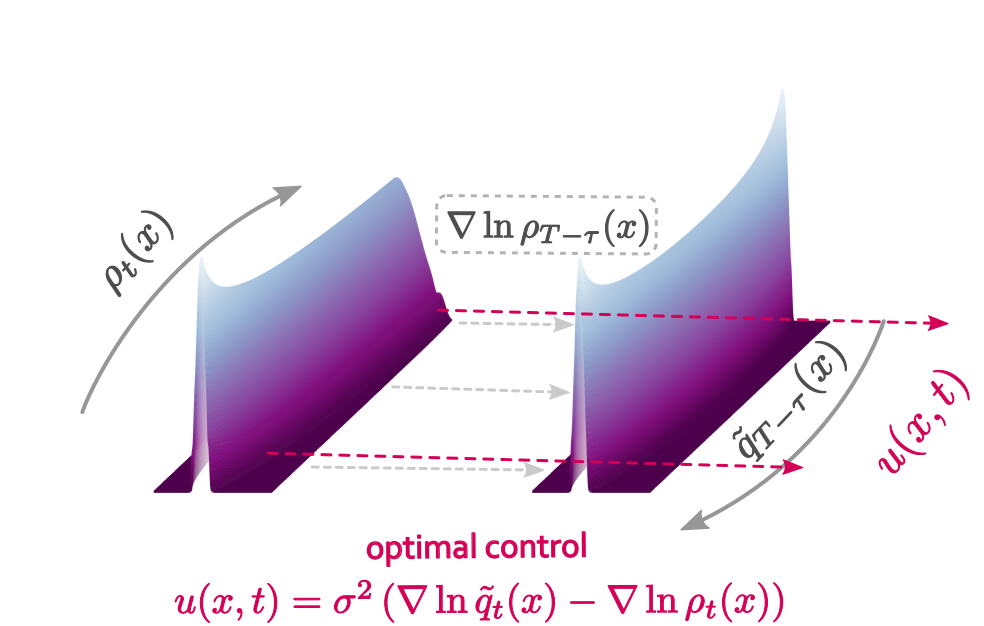
Devising optimal interventions for constraining stochastic systems is a challenging endeavour that has to confront the interplay between randomness and nonlinearity. Existing methods for identifying the necessary dynamical adjustments resort either to space discretising solutions of ensuing partial differential equations, or to iterative stochastic path sampling schemes. Yet, both approaches become computationally demanding for increasing system dimension. Here, we propose a generally applicable and practically feasible non-iterative methodology for obtaining optimal dynamical interventions for diffusive nonlinear systems. We estimate the necessary controls from an interacting particle approximation to the logarithmic gradient of two forward probability flows evolved following deterministic particle dynamics. Applied to several biologically inspired models, we show that our method provides the necessary optimal controls in settings with terminal-, transient-, or generalised collective-state constraints and arbitrary system dynamics.
PDF Abstract