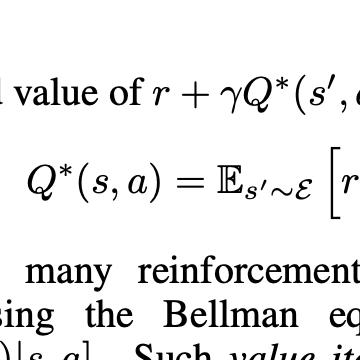Functional Stability of Discounted Markov Decision Processes Using Economic MPC Dissipativity Theory
This paper discusses the functional stability of closed-loop Markov Chains under optimal policies resulting from a discounted optimality criterion, forming Markov Decision Processes (MDPs). We investigate the stability of MDPs in the sense of probability measures (densities) underlying the state distributions and extend the dissipativity theory of Economic Model Predictive Control in order to characterize the MDP stability. This theory requires a so-called storage function satisfying a dissipativity inequality. In the probability measures space and for the discounted setting, we introduce new dissipativity conditions ensuring the MDP stability. We then use finite-horizon optimal control problems in order to generate valid storage functionals. In practice, we propose to use Q-learning to compute the storage functionals.
PDF Abstract